Cryptography/默克尔树
状态树在区块链中的作用
为了证明:
- 一个虚假交易在花费一笔不存在的 UTXO(UTXO 模型)
- 一个虚假交易被建立在一个虚假的 state root 上(账号模型)
- 轻节点中, 证明某个状态存在
Merkle Tree
首先, 让我们从默克尔树(Merkle Tree)的开始. 默克尔树提供了一种存储键值数据的方案, 我们首先对集合中的每个数据进行哈希处理, 然后继续沿树进行哈希处理, 直到到达根节点为止. 它的一个特点是快速重哈希: 当树节点内容发生变化时, 能够在前一次哈希计算的基础上, 仅仅将被修改的树节点进行哈希重计算, 便能得到一个新的根哈希用来代表整棵树的状态.
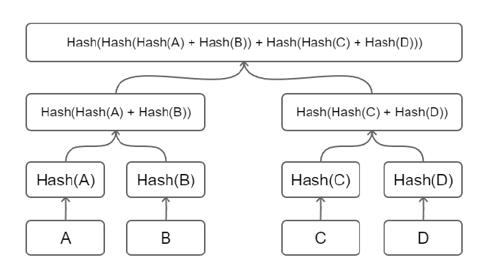
Merkle Proving
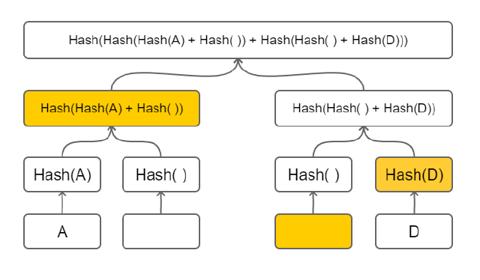
默克尔树的根只是一个哈希, 它"承诺"拥有某些数据, 但它并不实际告诉我们关于树的内容的任何信息. 我们可以使用一种称为默克尔证明(Merkle Prove)的手段来表明某些内容实际上是该树的一部分. 例如, 如果要证明 A 是树的一部分, 需要做的是:
- 提供 A 的原始内容
- 提供 Hash(B)
- 提供 Hash(Hash(C) + Hash(D))
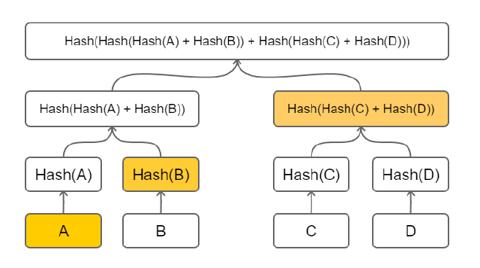
任何接收到以上信息的接收方, 都可以对提交的数据独立验证其计算结果是否等于已知的根哈希. 同时提出方只需要提供树的一部分而不必提供整颗树.
Trie
前缀树(Trie)又称为字典树, 是一种有序树, 用于保存关联数据. 其中的键通常是字符串. 与二叉查找树不同, 键不是直接保存在节点中, 而是由节点在树中的位置决定. 一个节点的所有子孙都有相同的前缀, 也就是这个节点对应的字符串, 而根节点对应空字符串.
如下是保存了字符串 "a", "b", "at", "atm", "ao" 的前缀树. 通常来说, 在实现前缀树的时候, 会在节点加入一个字段来表明其是否是一个完整单词.
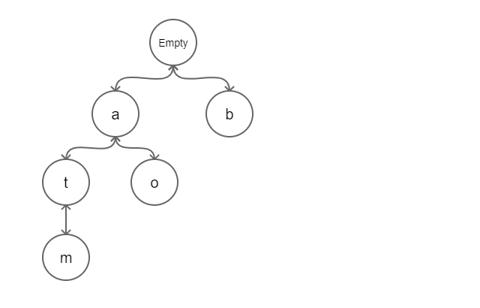
前缀树常用于搜索提示. 如当输入一个网址, 可以自动搜索出可能的选择. 当没有完全匹配的搜索结果, 可以返回前缀最相似的可能.
特性
- 相比于哈希表, 使用前缀树来进行查询拥有共同前缀的数据时十分高效, 例如在字典中查找前缀为 pre 的单词, 对于哈希表来说, 需要遍历整个表, 时间效率为 O(n), 然而对于前缀树来说, 只需要在树中找到前缀为 pre 的节点, 且遍历以这个节点为根节点的子树即可. 但是对于最差的情况(前缀为空串), 时间效率为 O(n), 仍然需要遍历整棵树, 此时效率与哈希表相同. 相比于哈希表, 前缀树不会存在哈希冲突的问题.
- 直接查找效率低下. 前缀树的查找效率是 O(m), m 为所查找节点的 key 长度, 而哈希表的查找效率为 O(1). 且一次查找会有 m 次 IO 开销, 相比于直接查找, 无论是速率还是对磁盘的压力都比较大.
- 空间浪费. 当存在一个节点其 key 值内容很长(如一串很长的字符串), 当树中没有与他相同前缀的分支时, 为了存储该节点, 需要创建许多非叶子节点来构建根节点到该节点间的路径, 造成了存储空间的浪费.
Radix Trie
压缩前缀树(Radix Trie)是一种更节省空间的前缀树. 其中作为唯一子节点的每个节点都与其父节点合并, 节点之间的边既可以表示为元素序列又可以表示为单个元素. 压缩前缀树更适用于对于较小的集合(尤其是字符串很长的情况下)和有很长相同前缀的字符串集合.
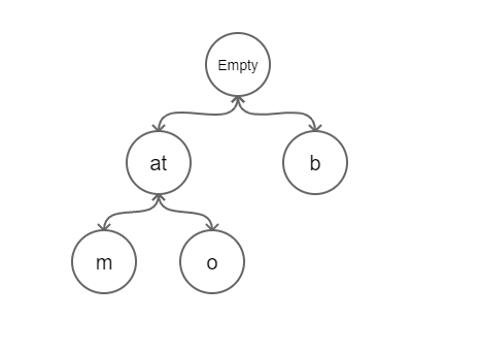
Merkle Patricia Tree
Merkle Patricia Tree 是以太坊 1.0 用于存储世界状态的数据结构, 它是一种经过改良且融合了 Merkle Tree 和 Radix Tree 两种树结构优点的数据结构. 它以 Radix Tree 为基础, 通过向数据结构添加一些额外的复杂性来解决效率低下的问题.
Merkle Patricia Trie 中的节点有如下的种类:
- NULL(表示为空字符串)
- Branch(分支节点), 总共有 17 子项, 为
[v0 ... v15, vt] - Leaf(叶子节点), 总共有 2 个子项, 为
[encodePath, value] - Extension(扩展节点), 总共有 2 个子项, 为
[encodePath, key]
Compact encoding of hex sequence with optional terminator
| hex char | bits | node type partial | path length |
|---|---|---|---|
| 0 | 0000 | extension | even |
| 1 | 0001 | extension | odd |
| 2 | 0010 | terminating (leaf) | even |
| 3 | 0011 | terminating (leaf) | odd |
以一个简单的例子来表示 MPT 的构建过程, 假设我们想要一个包含四个键值对的树: ('do', 'verb'), ('dog', 'puppy'), ('doge', 'coin'), ('horse', 'stallion'). 在构建过程中, 需要将 key/value 表示为 16 进制格式.
646f: 'verb'
646f67: 'puppy'
646f6765: 'coin'
686f727365: 'stallion'
其前缀树可表示如下:
6 -----> 46f ....................... 'verb'
| |----->67 ............. 'puppy'
| |-----> 65 .. 'coin'
|----> 86f727365 ................. 'stallion'
它的 MPT 树部分如下, 需要注意其键是经过 "Compact encoding of hex sequence with optional terminator" 的. 下图表示了 ('dog', 'puppy') 在树中的保存方式.
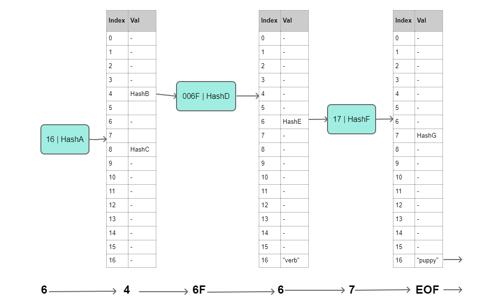
其整颗树以如下的键值对形式保存在数据库中:
rootHash: [ <16>, hashA ]
hashA: [ <>, <>, <>, <>, hashB, <>, <>, <>, hashC, <>, <>, <>, <>, <>, <>, <>, <> ]
hashC: [ <20 6f 72 73 65>, 'stallion' ]
hashB: [ <00 6f>, hashD ]
hashD: [ <>, <>, <>, <>, <>, <>, hashE, <>, <>, <>, <>, <>, <>, <>, <>, <>, 'verb' ]
hashE: [ <17>, hashF ]
hashF: [ <>, <>, <>, <>, <>, <>, hashG, <>, <>, <>, <>, <>, <>, <>, <>, <>, 'puppy' ]
hashG: [ <35>, 'coin' ]
Sparse Merkle Tree
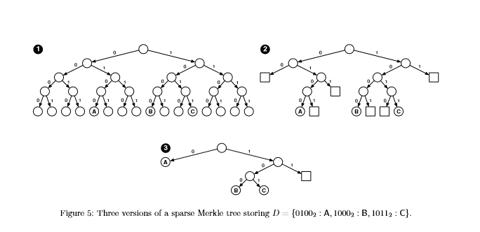
默克尔树可以证明一个数据包含在树中, 但它却无法证明一个数据不包含在树中. 稀疏的默克尔树(Sparse Merkle Tree)在这里发挥了作用. 稀疏的默克尔树类似于标准的默克尔树, 不同之处在于对包含的数据进行了索引, 并且每个数据点都放置在与该数据点的索引相对应的叶子上(即使这个叶子节点是空的).
为了证明 C 不存在树中, 只需要像标准默克尔树的存在证明一样证明 C 为空就行了!
特性
- 稀疏默克尔树真的非常稀疏, 因此需要花费大量的空间去存储它(2^256)!
- 由于不是前缀树, 访问一个 key 值需要更多的 db read 次数.
- 不但可以证明你拥有某个资产, 还可以证明你没有某个资产.
相关讨论
- https://ethereum.stackexchange.com/questions/57761/eli5-sparse-merkle-trees-on-sharding
- SMT 几乎可以在使用(或计划使用) Merkle Patricia Tries 的任何地方实现替换
- 以太坊的 MPT 的实施和使用都非常复杂, SMT 方式更简单, 效率也差不多
- https://ethresear.ch/t/data-availability-proof-friendly-state-tree-transitions/1453
- 文中指出默克尔树的一个问题, 即一个恶意矿工可以创建带有欺诈性 state root 的区块链, 该状态树根与该区块中的交易进行的状态转换不匹配, 因此没有人能够找到证明该树中包含任何状态的证据, 或者证明树中包含欺诈性的状态, 因为他们没有相关数据. 虽然可以通过提供整个状态树的数据可用性证明来防止这种情况, 但是, 这要求节点在每个块中广播系统的整个状态, 这当然不是很有效. 解决办法是在 Block Header 中包含多个中间 state root 而非一个最终的 state root.
- SMT 的优化的解决方案: https://www.links.org/files/RevocationTransparency.pdf, https://eprint.iacr.org/2016/683.pdf, 简单来说就是提前存储 Hash(Null), Hash(Hash(Null) + Hash(Null) ... ) ...
- SMT 的一个状态转换时间复杂度永远固定是 O(log(n)), 且 "Sparse merkle trees are used because they do not have to be rebalanced".
- Vitalik 在评论做了分析, 认为:
- Proof 证明的大小应该与 MPT 相当
- 从概念上, SMT 与 MPT 所能实现的功能几乎完全一样, 但胜在实现简单, 有巨大优势.
- https://www.deadalnix.me/2016/09/24/introducing-merklix-tree-as-an-unordered-merkle-tree-on-steroid/
- MPT 在集合的中间插入或删除一个元素将需要大量的运算, 如果需要 2 个包含相同元素的集合, 但是以不同的顺序插入将产生 2 个根本不同的树.
- 同一组元素总是会产生同样的根, 这对于很难维护一致性的系统非常重要, 这在分布式系统中很常见. 无论它们如何到达, 系统的节点最终都将收敛到相同的集合和相同的根.
- https://medium.com/@ouvrard.pierre.alain/sparse-merkle-tree-86e6e2fc26da
- SMT 可以并发更新键值. "The keys should be sorted in an array, and the corresponding values should be at the same index in a separate array", 相关代码实现在 https://github.com/aergoio/SMT.
- https://ethresear.ch/t/optimizing-sparse-merkle-trees/3751, SMT 的优化技巧
- zero branch 的预计算
- 如果有一个只有一个元素的子树, 我们可以简单地存储一条记录, 该记录说明值是什么, 键是什么以及哈希是什么(以避免必须重新计算). 它可以将 db read 操作次数降低至和 MPT 一样.
- 使用 Hex 作为键而非二叉树, 可以使 db read 次数降低 3-4 倍
- plasma 团队已经实现了该文章提高的全部优化
- Does the further design you describe require changing the on-chain verifier? No. The consensus rules are 100% the same, the hashes are 100% the same, the proofs are 100% the same, it’s a purely voluntary client-side change that different clients can implement differently. This is precisely why this is interesting.
- 如果约定 H(0, 0) = 0, 则是一个巨大的性能优化!
- https://github.com/ethereum/eth2.0-specs/issues/1472
SMT 在 Libra 中的实现
源码: https://github.com/libra/libra/tree/master/storage/jellyfish-merkle/src
Libra SMT 一共有三种节点, 与 MPT 基本一致.
- Branch
- Extension
- Leaf
由于添加了叶节点, 并且 Branch 是前缀式的, 以太坊社区将之称为"稀疏紧凑型默克尔树"(两个反义词在一起却毫无违和感, 居然还能理解是什么意思...).